
公開日:2023年04月05日
/
更新日:2024年04月16日
情報セキュリティコラム第4回、今回のテーマは「RSA暗号」です。
RSA暗号とは、2つの素数を使って暗号化と復号を行う仕組みです。暗号化とは、元のデータや通信内容を第三者や外部から解読できない状態にする処理のことを指します。反対に、暗号化されたデータを元のデータに戻すことを復号と呼びます。
この技術は、皆さんの日常生活や仕事の中でも利用されていて、第三者への情報漏洩や改ざんの防止に役立っています。
このRSA暗号は、どんな仕組みでしょうか。今回はその検証(復号=暗号を解く)とともに、仕組みを解説します。暗号化技術の理解の参考になれば幸いです。
そもそも暗号とは
もともと暗号は、古来より第三者に盗み見られた時に備えて、情報を隠蔽化するものとして使われてきました。機密を扱うために使われることが多かったのですが、古来の暗号は法則性が分かると解読できてしまう「換字式暗号」でした。そのため、コンピューターの計算能力が向上した現代で使われることは殆どなくなっています。
RSA暗号
RSA暗号は、1977年に発明されてから、現在でも高い強度を誇るアルゴリズムです。インターネットのSSL証明書を利用した暗号化通信で利用されていて、セキュリティ対策には欠かせない、大きな役割を持つ暗号です。
高強度の理由は至ってシンプルです。RSA暗号は巨大な桁の素数を使っています。それらを素因数分解することは非常に困難であり、コンピューターで計算しても天文学的な時間が必要になり、非現実的な回数の試行が必要になるからです。スーパーコンピュータや量子コンピューター並みの計算能力と膨大な時間が必要になります。
RSAの鍵生成手順
では、実際どのくらい高強度なのか、鍵の生成手順を見てみましょう。

用語解説
- 秘密鍵
- 暗号データを復号する際に使う鍵。特定のユーザーのみが所持。
- 公開鍵
- 通信を暗号化する際に必要な鍵。
- オイラー関数
- 自然数nと互いに素なn以下の自然数の個数をφ(n)で表す関数。
- ユークリッド互除法
- 2つの自然数の最大公約数を求める手法の一つ。
暗号化のしくみ
次に、生成した鍵、いわゆる「公開鍵」「秘密鍵」をもとに暗号化と復号を検証してみます。
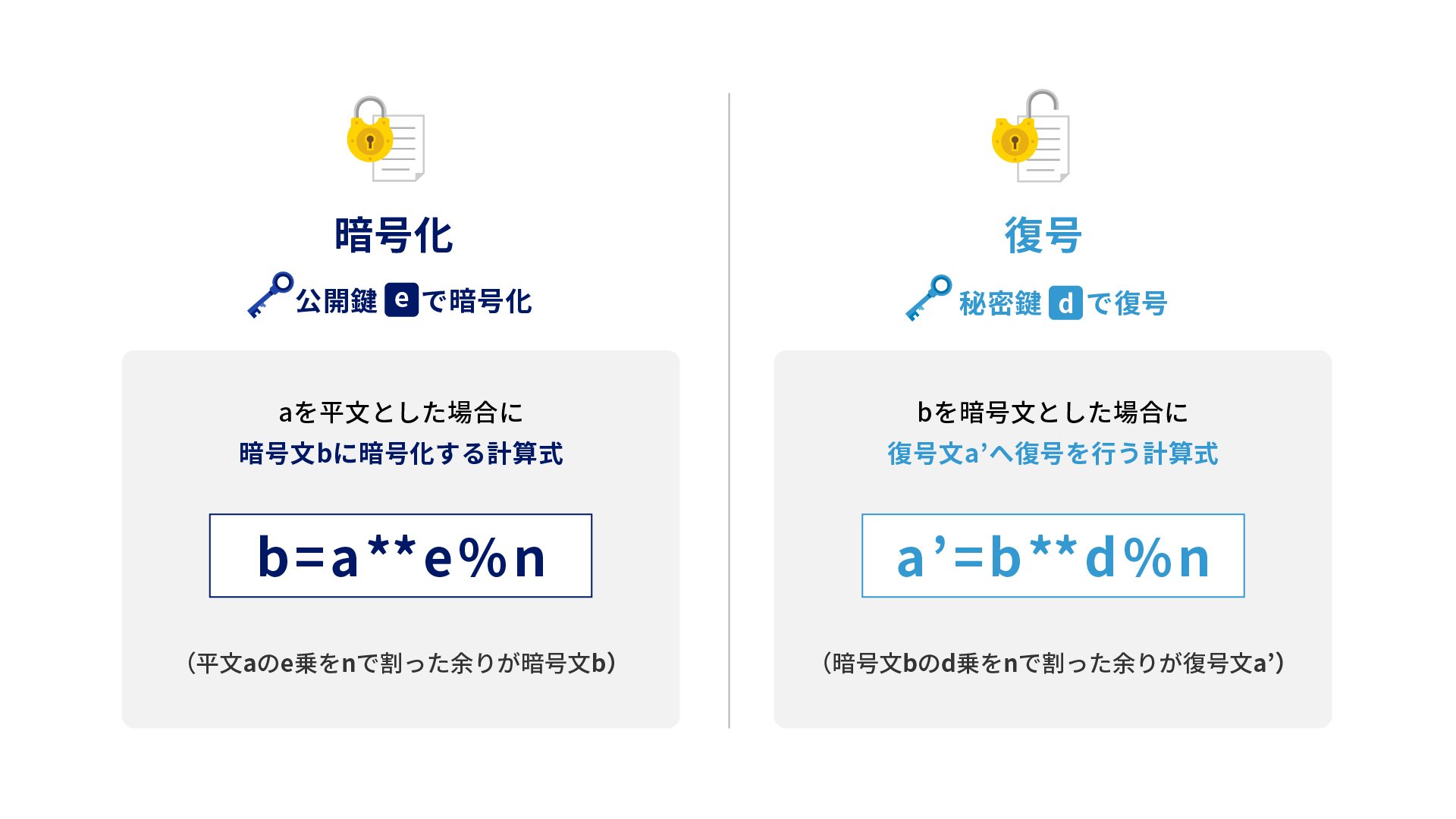
実際に文字列を公開鍵で暗号化して、秘密鍵で復号してみます。
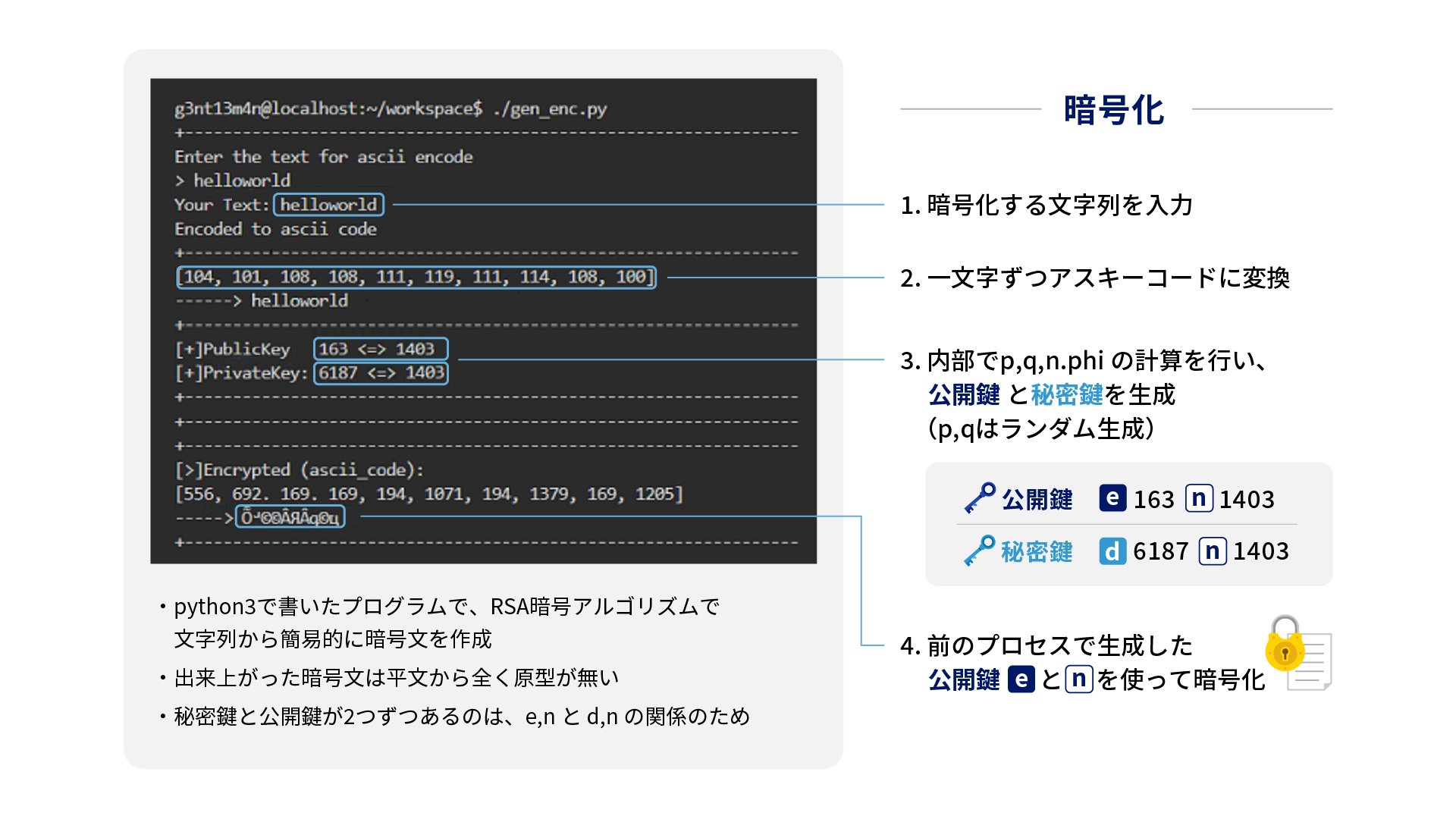
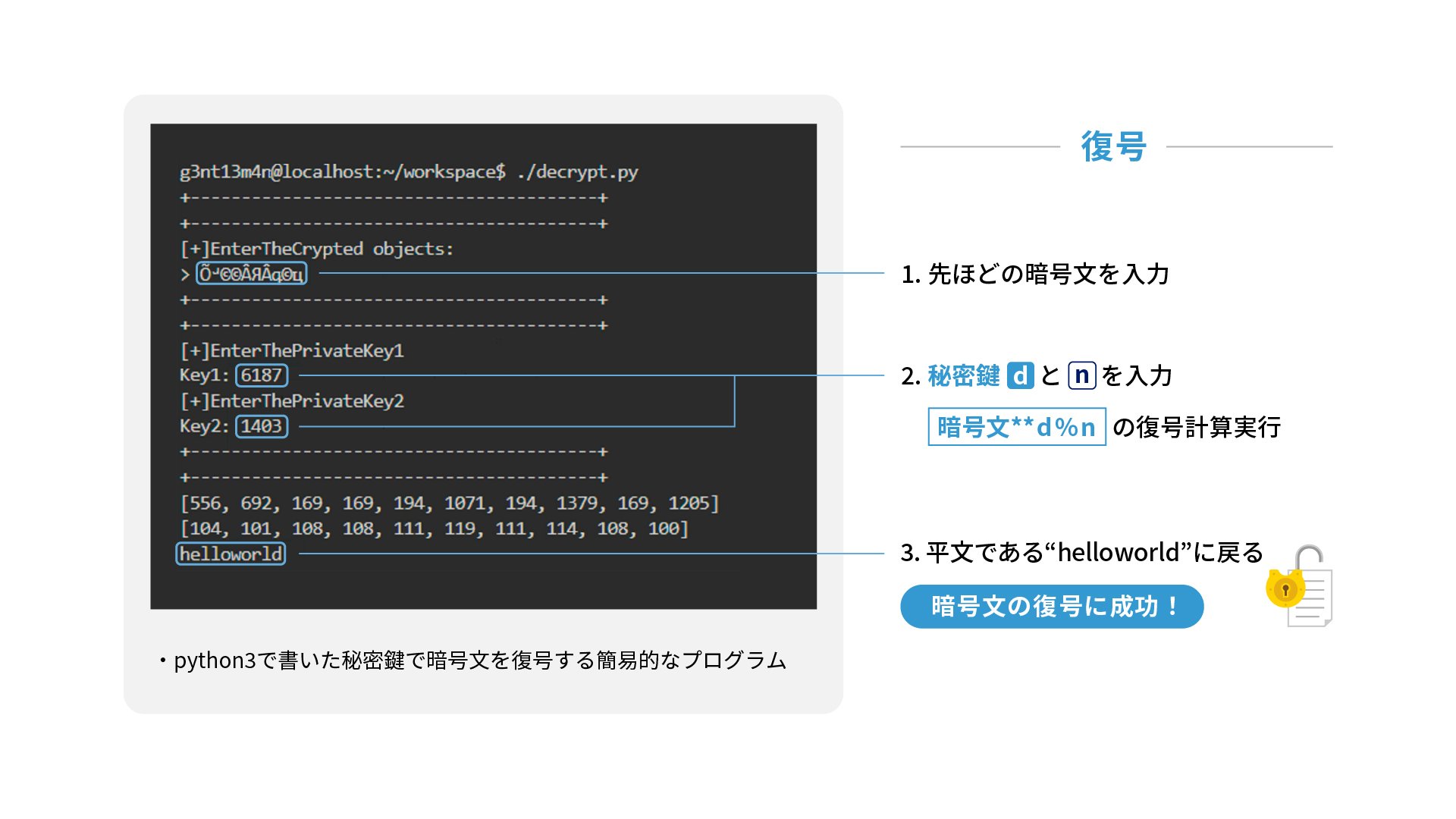
秘密鍵を持っていれば、無事に復号できます。
実際には公開鍵は名前のとおり公開されても問題はなく、暗号文は秘密鍵を持っている人しか復号ができません。
もしこれを総当たりで無理矢理復号していく場合、ひたすら秘密鍵「d」として有効と思われる素数を試行していくことになりますが、手がかりなく行うことは無理難題といえます。
まとめ
RSA暗号が高強度・安全といわれる所以は、秘密鍵無しに素因数分解していくことが無理難題ということに起因しています。今回のコラムが、私たちの生活に身近なRSA暗号の理解の参考になりましたら幸いです。
ここまでお読みいただきありがとうございました。次回コラムは5月中旬更新予定です。


